SDSC5003

ER Design

constraints策略

One or Many?

ER图的一对一、多对多关系箭头怎么画？

假设A->B中，A只能对应一个B，那么A画到关系中需要加箭头，反过来相同

Participation Constraints

参与是可以是完全（存在约束）或部分（无约束）的

完全参与的关系必须使用双实线进行连接

eg：Children attend pre-school, assume that

• Children can only attend one pre-school
• A pre-school must have children

eg:Employees work for companies

• An employee must be employed by someone (or they wouldn’t be an

employee) 每个员工都必须有公司，必须实现works_for

• People often have more than one job 每个员工都必须有员工
• 二者没有one
• 的限制，即多对多

Extended ER Model

Weak Entities 弱实体

弱实体简单来说就是完全依赖另一方的实体

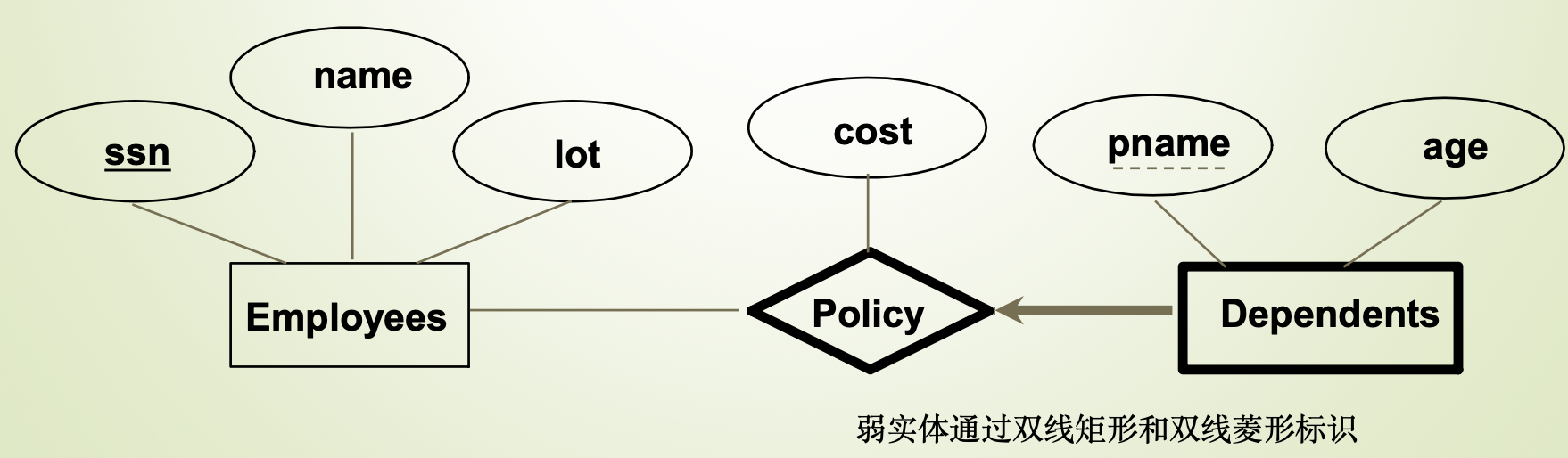
ISA (‘is a’) Hierarchies 继承

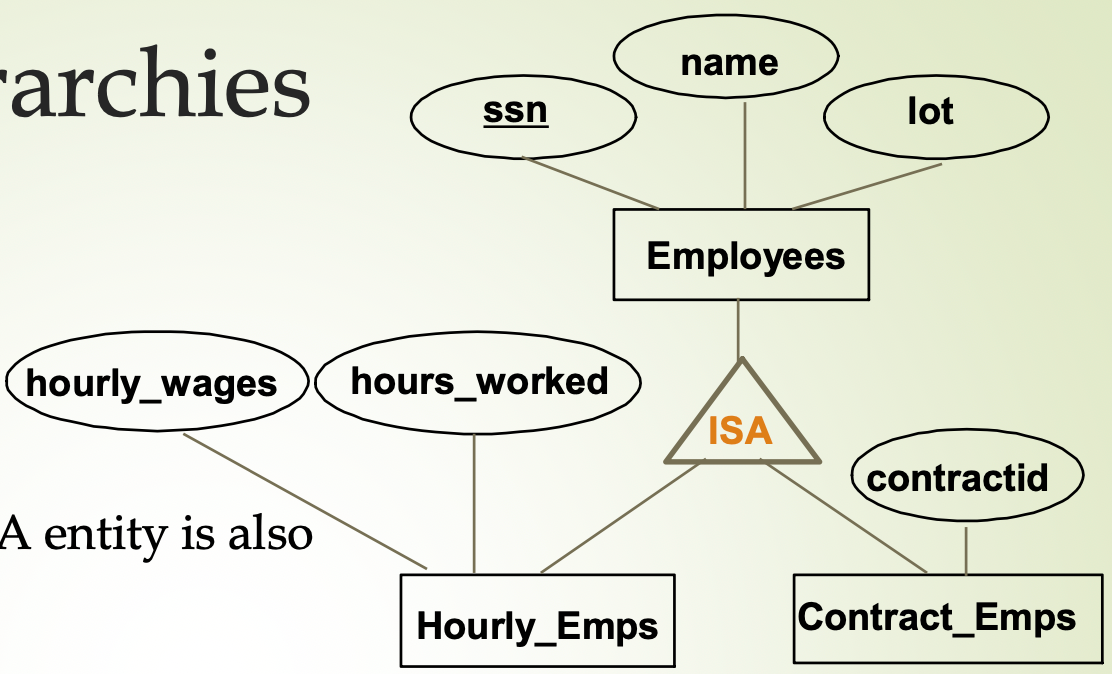
Aggregation 聚和

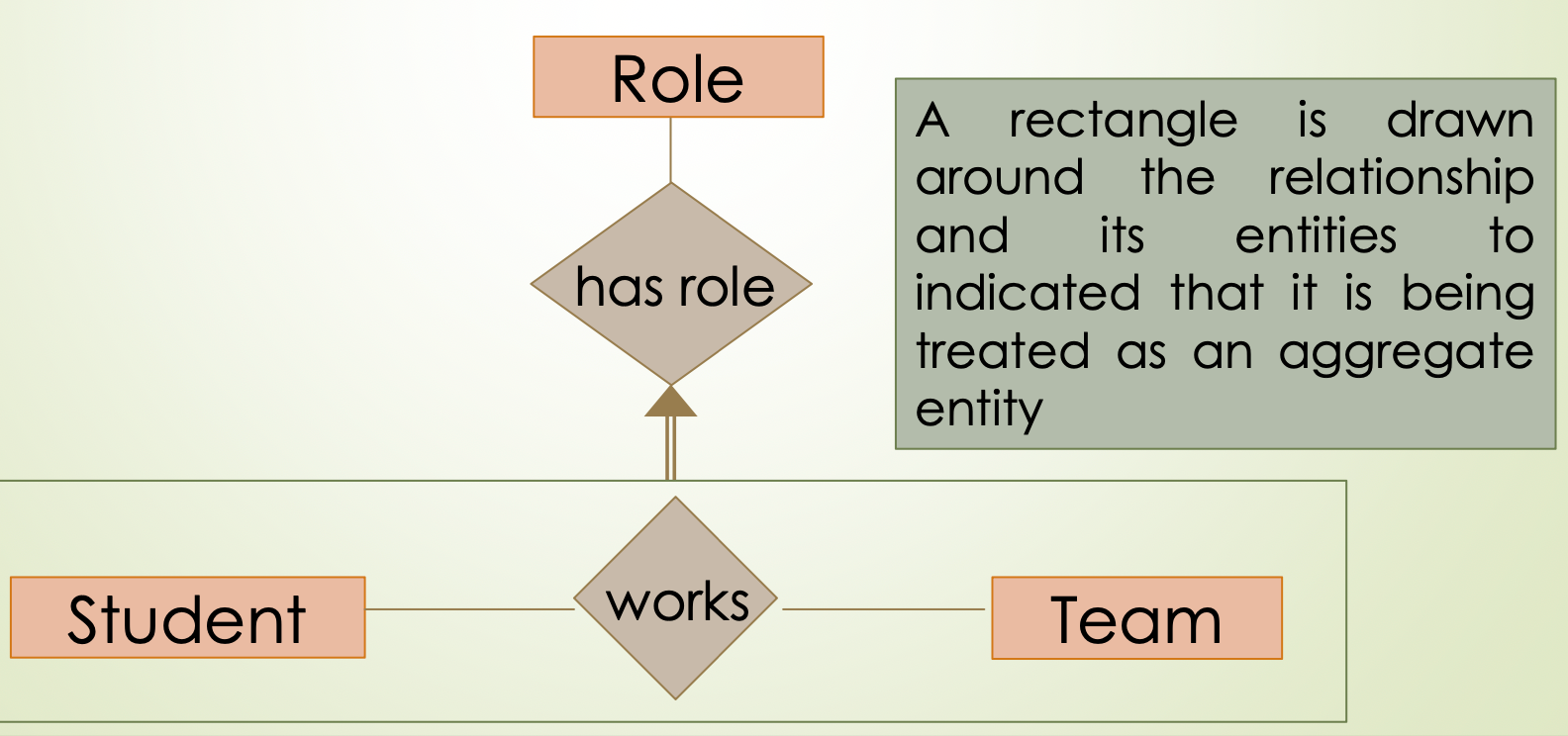
ER-to-SQL

删除策略

CREATE TABLE 子表 (
    id INTEGER PRIMARY KEY,
    main_id INTEGER,
    -- 外键约束，联级删除
    FOREIGN KEY (main_id) REFERENCES 主表(id) ON DELETE CASCADE
);

• CASCAD
  ON DELETE CASCADE
• SET NULL
  ON DELETE SET NULL
• SET DEFAULT + ON DELETE SET DEFAULT
• RESTRICT 如果从表中有引用该记录的数据，删除操作会被阻止
  ON DELETE RESTRICT

基本方法

对于强制是否存在，主要靠外键是否为空+删除策略来规定

一对一 两方必须存在/一对一 一方必须存在

每一个实体都对应转化为一张SQL表，并选择“可以容忍自己没有对应元素”作为主表（因为主表不存外键），把它的主键放入另一个实体对应的SQL表中作为外键，外键不允许为空，联级删除选择CASCAD

一对一 两方都可选

任意选择一张表为主表，把它的主键放入另一个实体对应的SQL表中作为外键，外键允许为空，联级删除选择 SET NULL

一对多 两实体都为强制存在 / WEAK ENTITES

将 多 的实体（例如在部门员工表中：一个员工只能指向一个部门，一个部门可以被多个员工指，此时部门就是“多”）设置为主表，把它的主键放入另一个实体对应的SQL表中作为外键，外键不允许为空，联级删除选择CASCAD

一对多 两方都可选

将 多 的实体设置为主表，把它的主键放入另一个实体对应的SQL表中作为外键，外键允许为空，联级删除选择 SET NULL

多对多

需要一张新关系表包含两个实体的主键。无论两边实体是否为可选存在的，其转化形式一致，关系表中的外键列不能为NULL。

Relational Algebra

Relational Algebra Operations

• Basic operations:
  • Selection ($\sigma$): Selects a subset of rows from a relation.
    • ${\sigma }_{Iname=Summer}(Customer)$
  • Projection ($\pi$): Selects a subset of columns from a relation. 选择列
  • Cross-product ($\times$): Allows us to combine two relations.
  • Set-difference ($-$): Tuples in relation 1, but not in relation 2.
  • Union ($\cup$): Tuples in relation 1 and in relation 2.
• Additional derived operations:
  • Intersection
  • join （$\bowtie$） eg：$S1{\bowtie }_{S1.sid<R1.sid}R1$ from S1, R1 where S1.sid<R1.sid
  • division ($÷$)
  • renaming ($C$/$\rho$ ) eg: ${\rho }_{newName/oldName}(Relation)$
    • Not essential, but very useful.
• Note: Since each operation returns a relation, operations can be composed! 注意：每个操作都返回关系，因此可以组合操作！

Natural Join

Equi-join on all common fields. 在所有共同字段上进行等值连接。

Division

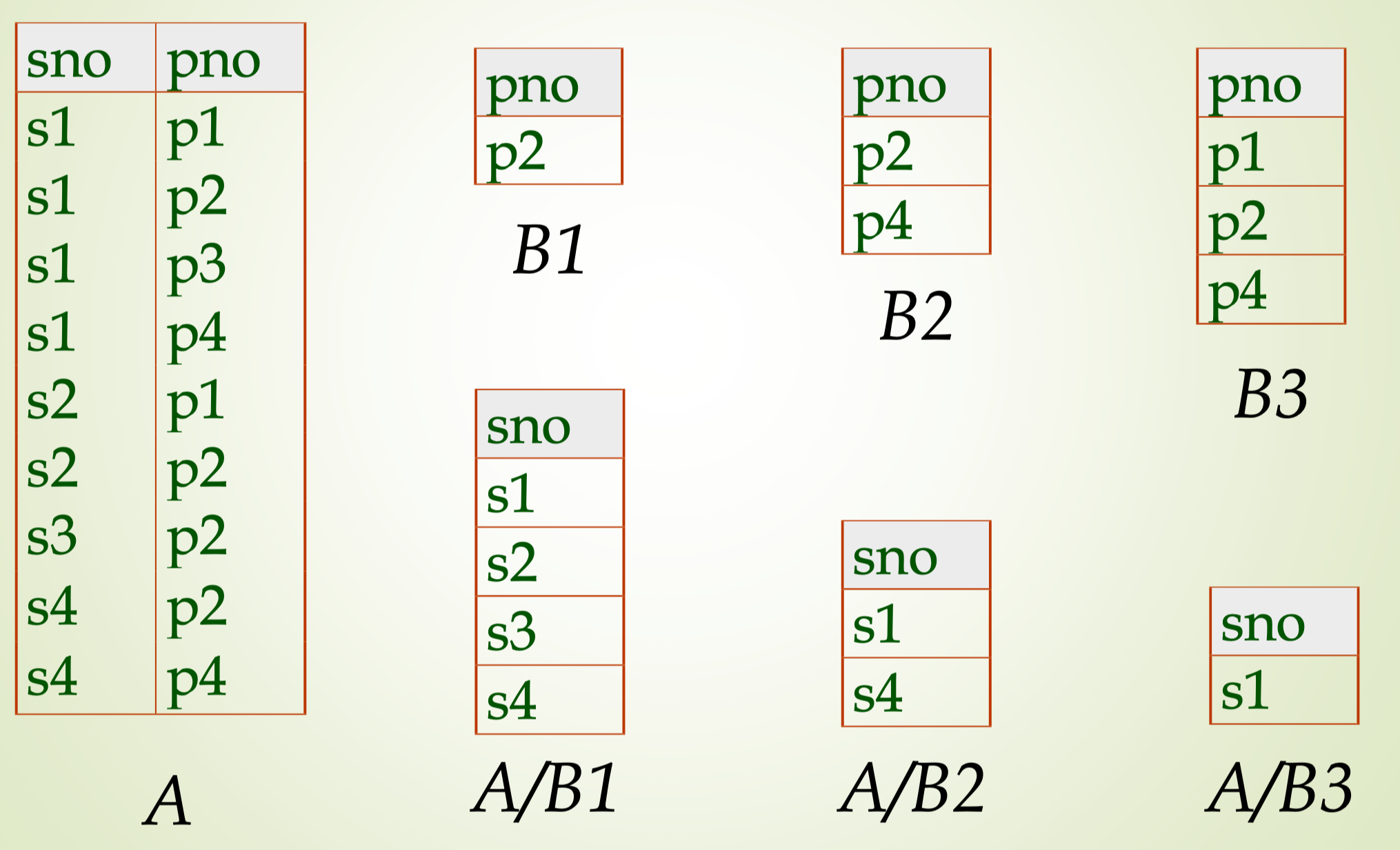
eg: Find the names of sailors who’ve reserved all boats

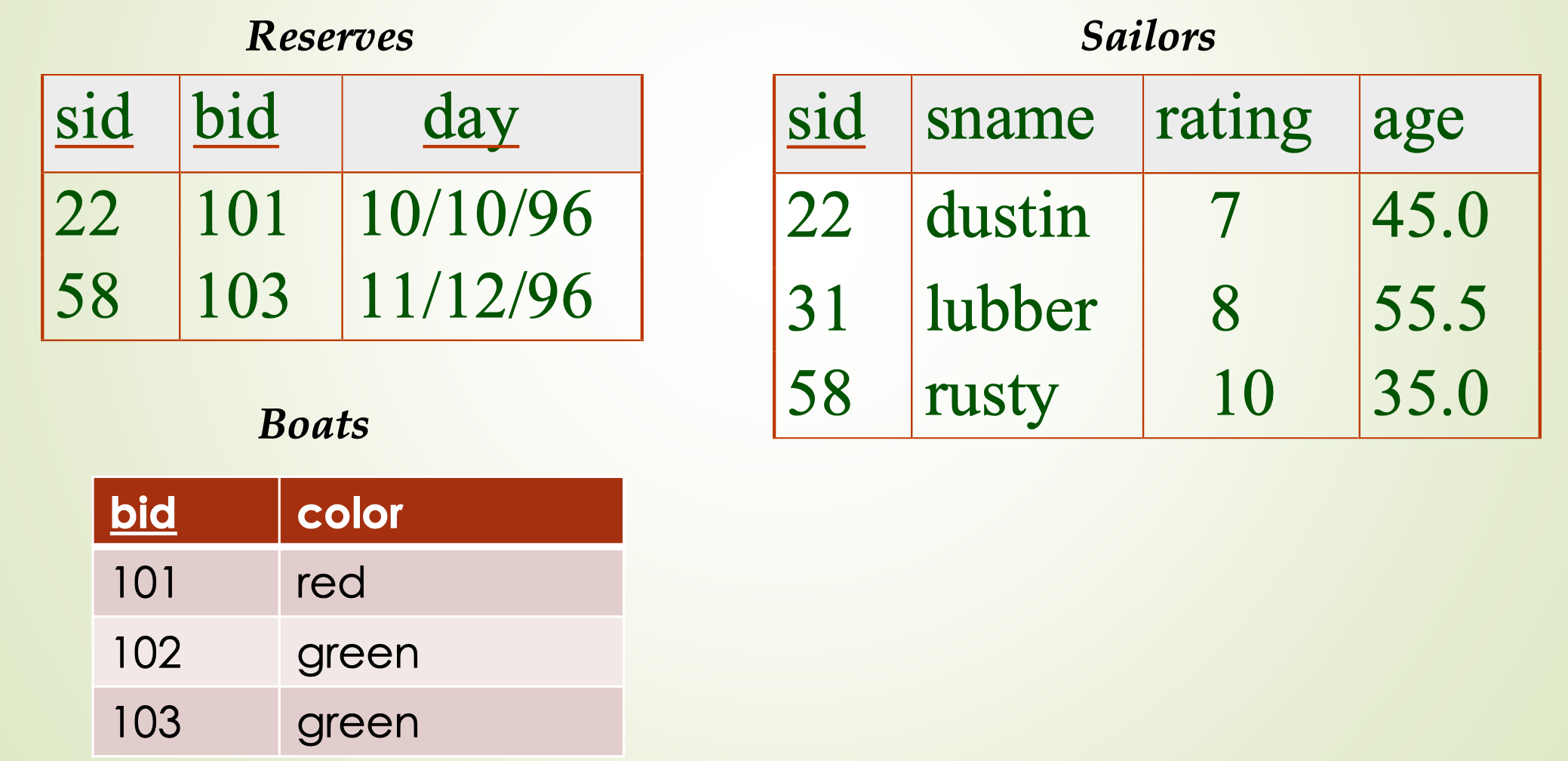
利用除法实现查找“所有”的功能

${\pi }_{\text{sid}}(\text{Reserves})÷{\pi }_{\text{bid}}(\text{Boats})$

Skills

How to use algebra to expree select max(value) from T group by name ?

使用笛卡尔积+减

$$\begin{gathered} A:={\pi }_{name,value}(T) \\ B:={\rho }_{(name,value,nam{e}^{\prime },valu{e}^{\prime })}(T\times T) \\ C:={\pi }_{name,value}({\sigma }_{name=nam{e}^{\prime }\text{and}value<valu{e}^{\prime }}(B)) \\ Result=A-C \end{gathered}$$

How to translate algebra $÷$ to SQL?

1. Table A (EmployeeSkills): Stores EmployeeID and Skill each employee possesses.

2. Table B (RequiredSkills): Stores Skill values that represent the required skills.

SELECT DISTINCT A.EmployeeID
FROM EmployeeSkills A
WHERE NOT EXISTS (
    SELECT *
    FROM RequiredSkills B
    WHERE NOT EXISTS (
        SELECT *
        FROM EmployeeSkills A2
        WHERE A2.EmployeeID = A.EmployeeID
          AND A2.Skill = B.Skill
    )
);

or using inner join and count(distinct )

SELECT A.EmployeeID
FROM EmployeeSkills A
JOIN RequiredSkills B ON A.Skill = B.Skill
GROUP BY A.EmployeeID
HAVING COUNT(DISTINCT A.Skill) = (SELECT COUNT(*) FROM RequiredSkills);

Design Theory

Target

Avoid anomalies 避免异常

Anomaly Kinds

• 数据冗余 redundant
• 更新异常 update anomaly
• 删除异常 delete anomaly
• 插入异常 insert anomaly

Normal Forms

• 1NF: All table are flat
• 2NF: 1NF & No non-prime attribute FD part candidate key 要求实体的属性完全依赖于主关键字
• 3NF: 2NF & no Transitive Dependency 无传递依赖
• BCNF: no bad FDs

Functional Dependency (FD)

We write $A\to B$ or say $A$ functionally determines $B$ if,

for any tuples $t1$ and $t2$ :

$t1[A]=t2[A]impliest1[B]=t2[B]$

and we call $A\to B$ a functional dependency

A的值可以直接决定B的是什么，则B依赖于A

example

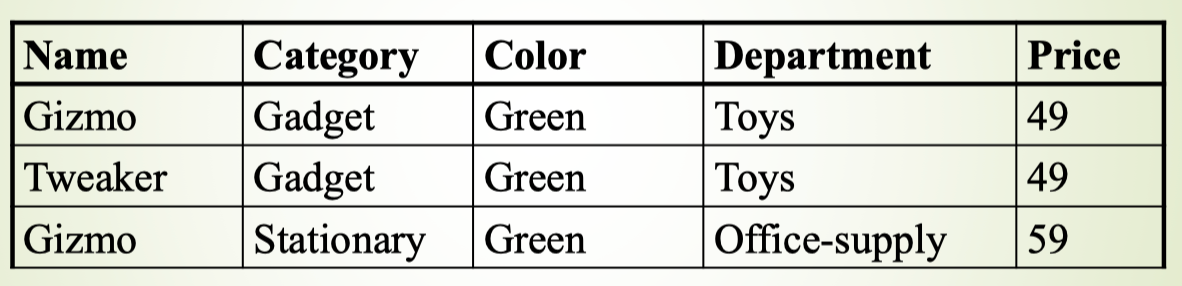
• Name -> Color : FD holds
• Name -> Price : FD dose not hold eg: Gizmo have two diff Departments
• Category -> Department : DF holds
• Color, Category -> Price

Because of Name -> Color Category -> Department Color, Category -> Price We can infer that Name, Category -> Price, 可以看出一种传递依赖

Inferred FDs

Split/Combine

$$\begin{array}{rl}& A_1,\dots ,A_m\to B_1,\dots ,B_n\\ & \text{is equivalent to the following }n\text{ FDs:}\\ & A_1,\dots ,A_m\to B_i\text{for }i=1,\dots ,n\end{array}$$

And vice-versa

$$\begin{array}{rl}& A_1,\dots ,A_m\to B_i\text{for }i=1,\dots ,n\\ & \text{is equivalent to the following }n\text{ FDs:}\\ & A_1,\dots ,A_m\to B_1,\dots ,B_n\end{array}$$

Reduction/Tricial

$$A_1,\dots ,A_m\to A_j\text{for any }j=1,\dots ,m$$

Transitive

$$\begin{array}{rl}& A_1,\dots ,A_m\to B_1,\dots ,B_n\text{ and }{B}_1,\dots ,B_n\to C_1,\dots ,C_k\\ & \text{implies}\\ & A_1,\dots ,A_m\to C_1,\dots ,C_k\end{array}$$

example

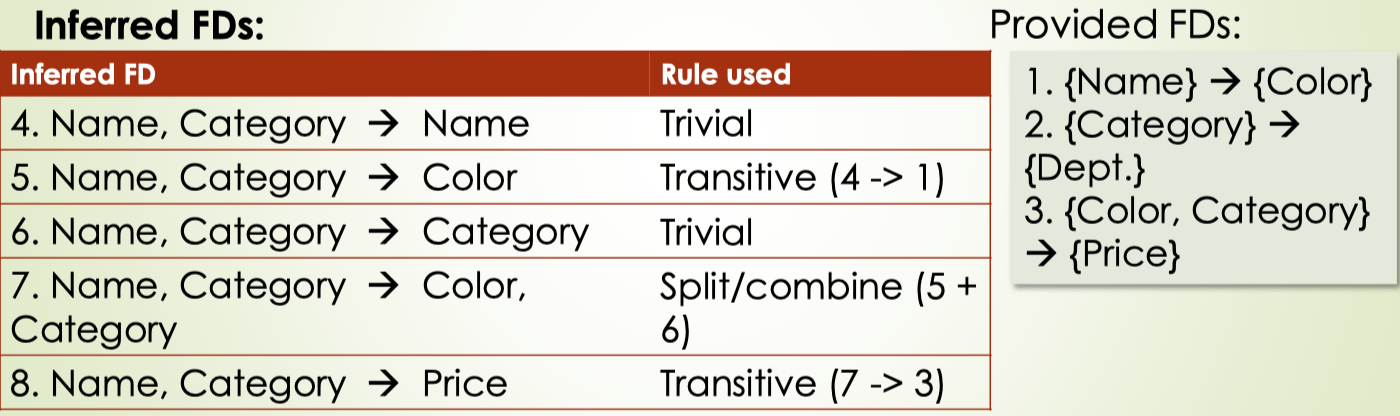
Closure

example

$$\mathbf{\text{Example:}}F=\{\begin{array}{l}\text{name}\to \text{color}\\ \text{category}\to \text{department}\\ \text{color, category}\to \text{price}\end{array}$$$$\begin{gathered} \mathbf{\text{Closures:}} \\ \begin{array}{rl}& \{\text{name}{\}}^{+}=\{\text{name, color}\}\\ & \{\text{name, category}{\}}^{+}=\{\text{name, category, color, dept, price}\}\\ & \{\text{color}{\}}^{+}=\{\text{color}\}\end{array} \end{gathered}$$

Algorithm to find $X^{+}$

$$\begin{array}{rl}& \mathbf{\text{Start }}withX=\{A_1,\dots ,A_n\},\text{ FDs }F.\\ & \mathbf{\text{Repeat until}}\text{ X doesn’t change;}\\ & \mathbf{\text{do:}}\\ & \mathbf{\text{if}}\{B_1,\dots ,B_n\}\to C\text{ is in }F\\ & \mathbf{\text{and}}\{B_1,\dots ,B_n\}\subseteq X:\\ & \mathbf{\text{then}}\text{ add }C\text{ to }X.\\ & \mathbf{\text{Return}}X\text{ as }{X}^{+}.\end{array}$$

Non-trivial FD

非平凡函数依赖（non-trivial functional dependency）是指函数依赖 $X\to Y$ 中的右手边 Y 不包含在左手边 X 中的情况。换句话说，Y 中的元素不在 X 中出现

Exercise - find all FDs implied by the given FDs

Find all non-trivial functional dependency implied by

$$\begin{array}{rl}A,B& \to C\\ A,D& \to B\\ B& \to D\end{array}$$

Requirements:

1. Non-trivial FDs (we avoid reflexive dependencies like $A,B\to A$ ).
2. Each FD must have a single attribute on the right-hand side.

Solove:

1. Compute Attribute Closures, and get new FDs from Closures by Inferred FDs methods, especially using Split

2. Identify Non-Redundant FDs

https://chatgpt.com/share/671ffa9a-e5b8-8008-820b-ddbb74006e93

FDs to Candidate keys

按以下步骤求Candidate keys：

1. 只在FD右部出现的属性，不属于候选码;
2. 只在FD左部出现的属性，一定存在于某候选码当中;
3. 其他属性逐个与2,3的属性组合，求属性闭包，直至X的闭包等于U(全部元素),若等于U,则X为候选码。

“Good” vs. “Bad” FDs

What is “Bad” FDs? and what is 2NF/3NF/BFNF?

• Partial Dependency 部分依赖 (2NF) ：

某些非主属性依赖于主键的一部分，而不是整个主键

$$\begin{array}{rl}A,B& \to C\\ B& \to D\text{ (Bad FDs)}\end{array}$$

• Transitive Dependency 传递依赖 (3NF)：

3NF:

• First, it should be in 2NF
• No non-prime attribute非主属性 should be transitively dependent on the Key of the table.

非主属性依赖于另一个非主属性，而这个非主属性又依赖于主键

X is prime attribute, Y Z is non-prime attribute:

$$\begin{array}{rl}X& \text{ is Primary key}\\ X& \to Y\\ Y& \to Z\text{ (Bad FDs)}\end{array}$$

• Non-Candidate Key Dependencies 存在非候选键依赖项 （BCNF）：

存在非平凡函数依赖的左手边（决定因素）不是是候选键的情况

$$\begin{array}{r}\\ A,B& \to C\text{ (A and B}\text{ is Primary key)}\\ C& \to A\text{ (Bad FDs, because C is not Primary key)}\end{array}$$

BCNF Decomposition Algorithm

$$\begin{array}{rl}& \mathbf{\text{BCNFDecomp(R):}}\\ & \text{Find a non-trivial bad FD: }X\to Y\\ & \mathbf{\text{if}}\text{(not found) }\\ & \mathbf{\text{then Return}}R\\ & \mathbf{\text{Split}}R\text{ into }{X}^{+}\text{and }[X+[\text{rest attributes}]]\\ & \text{ as }{R}_1\text{ and }{R}_2\\ & \mathbf{\text{Return }}\text{BCNFDecomp}(R_1),\text{BCNFDecomp}(R_2)\end{array}$$

example

$$\begin{array}{rl}R(A,B& ,C,D,E)\\ \{C\}& \to \{D\}\\ \{A\}& \to \{B,C\}\end{array}$$

BCNFDecomp(R(A, B, C, D, E)):
for FD:
  1.try {C} -> {D}
    C+ = {C, D} 
    as for R(A, B, C, D, E)
      {C, D} in C+, {A, B, E} not in C+ 
    split R(A, B, C, D, E) into
      R(C, D) and R(C, A, B, E)
    return BCNFDecomp(R(C, D)) 
      and BCNFDecomp(R(A, B, C, E))
      		
      		
BCNFDecomp(R(C, D)):
for FD:
  1.try {C} -> {D}
    C+ = {C, D} 
    as for R(C, D)
    	{C, D} in C+, {} not in C+ 
    can't split
    
  2.try {A} -> {B,C}
  	A+ = {A, B, C, D}
  	as for R(C, D)
  		{C, D} in A+, {} not in A+ 
  		can't split
  		
  return R(C, D)
  
  
BCNFDecomp(R(A, B, C, E)):
for FD:
  1.try {C} -> {D}
    C+ = {C, D} 
    as for R(A, B, C, E)
      {C} in C+, {A, B, E} not in C+ 
    can't split, because split is meanless
    
  2.try {A} -> {B,C}
  	A+ = {A, B, C, D}
  	as for R(A, B, C, E)
  		{A, B, C} in A+, {E} not in A+ 
    split R(A, B, C, D, E) into
      R(A, B, C) and R(A, E)
    return BCNFDecomp(R(A, B, C)) 
      and BCNFDecomp(R(A, E))
      
      
BCNFDecomp(R(A, B, C)):
for FD:
  1.try {C} -> {D}
    C+ = {C, D} 
    as for R(A, B, C):
    	{C} in C+, {A, B} not in C+ 
    can't split, because split is meanless
    
  2.try {A} -> {B,C}
  	A+ = {A, B, C, D}
  	as for R(A, B, C):
  		{A, B, C} in A+, {}
			can't split
			
  return R(A, B, C)
			
			
BCNFDecomp(R(A, E)):
  1.try {C} -> {D}
    C+ = {C, D} 
    as for R(A, E):
    	{} in C+, {A, E} not in C+ 
    can't split
    
  2.try {A} -> {B,C}
  	A+ = {A, B, C, D}
  	as for R(A, E):
  		{A} in A+, {E} not in A+
			can't split, because split is meanless
			
  return R(A, E)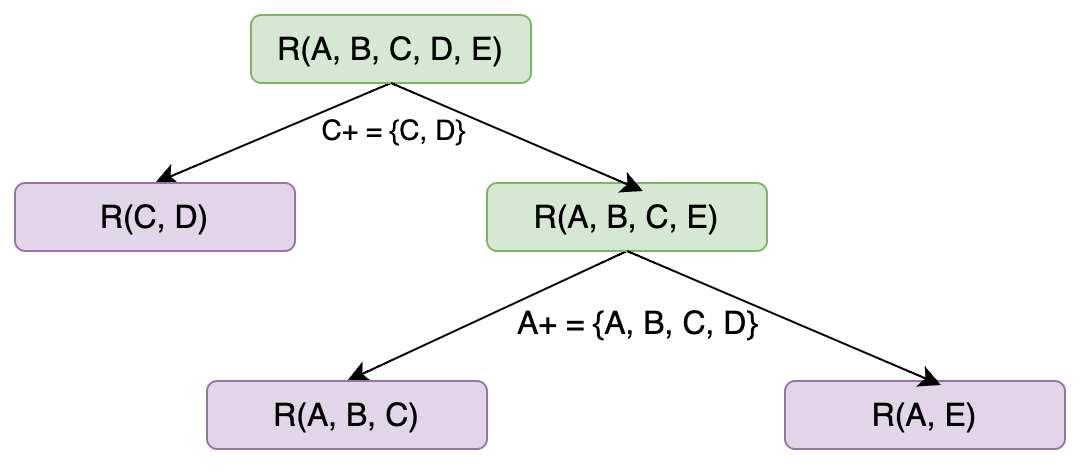

Answer: {C, D} {A, B, C} {A, E}

A Problem with BCNF

$$\begin{array}{rl}A& \to B\\ B,C& \to A\end{array}$$

If we use BCNFDecomp(R(A, B, C)) : {A, B} {A, C}

We lose the FD : $B,C\to A$

THE ANSWER IS THAT: One can always losslessly decompose to 3NF while preserving FDs but BCNF might not preserve them. 3NF的转换可以做到无损，但是BCNF可能会丢失依赖

Refrence: https://stackoverflow.com/questions/23965143/converting-3nf-to-bcnf-when-there-is-a-circular-dependency

Indexing

方式	数据存储形式
Alternative (1)	<A, rid>
Alternative (2)	<A, (B, C)>
Alternative (3)	<A, L>
rid 是指向记录的唯一标识符（Record ID）
A 是索引键（Search Key），(B, C) 是物理位置的具体描述：
• B 表示数据所在的页号（Page Number）
• C 表示数据在页内的偏移量（Slot/Location）
L 是记录 rid 的列表（List of Record IDs）