STATISTICS

Random variables

A random variable is a function that assigns a numerical value to each possible outcome of a random experiment, capturing important aspects of those outcomes in a simplified form.

Discrete vs. Continuous

• Discrete 离散的: If the random variable has a finite or countably infinite set of values (e.g., count of allergic reactions), it’s discrete.

• Continuous: If it can take any real number in a range, it’s continuous.

Example:

In a dice game, let X be the outcome of a single roll. Here, X can be any integer from 1 to 6.
In a study measuring people’s heights, let Y represent the height of a randomly selected person. Here, Y is continuous, as it can take on any value within a range (e.g., 150 cm to 200 cm).

A random variable is usually denoted by a capital letter (e.g., X , Y ), and its specific values are represented by lowercase letters (e.g., X = 3 means the random variable X takes the value 3).

$X (s) = t$ means that the random variable X assigns the value $t$ to the sample outcome $s$ .

Binomial distribution

Probability Formula for the Binomial Distribution

The probability of having exactly $k$ successes in $n$ trials is given by:

P (X = k) = (\binom{n}{k}) p^{k} (1 - p)^{n - k}

where:

$P (X = k)$ is the probability of getting exactly k successes.
$(\binom{n}{k}) = \frac{n!}{k! (n - k)!}$ is the binomial coefficient (number of ways to choose k successes from n trials).
$p$ is the probability of success on each trial.
$1 - p$ is the probability of failure on each trial.
$n - k$ is the number of failures.

example1

An information technology center uses nine aging disk drives for storage. The probability that any one of them is out of service is 0.06. For the center to function properly, at least seven of the drives must be available. What is the probability that the computing center can get its work done？

(\binom{9}{7}) (0.94)^{7} (0.06)^{2} + (\binom{9}{8}) (0.94)^{8} (0.06)^{1} + (\binom{9}{7}) (0.94)^{9} (0.06)^{0} = 0.986

example2

Kingwest Pharmaceuticals is experimenting with a new affordable AIDS medication, PM-17. Thirty monkeys infected with the HIV complex have been given the drug. Any inexpensive drug capable of being effective 60% of the time would be considered a major breakthrough; medications whose chances of success are 50% or less are not likely to have any commercial potential.

Kingwest hopes to avoid making either of two errors:

(1) rejecting a drug that would ultimately prove to be marketable 拒绝一种最终会被证明可以上市的药物 and (2) spending additional development dollars on a drug whose effectiveness, in the long run, would be 50% or less.花费额外的研发费用购买一种从长远来看疗效只有 50%或更低的药物。

As a tentative “decision rule,” the project manager suggests that unless sixteen or more of the monkeys show improvement, research on PM-17 should be discontinued.

a. What are the chances that the “sixteen or more” rule will cause the company to reject PM-17, even if the drug is 60% effective?

Assume $p = P (s u c c e s s) = 0.60$ , we have 30 monkeys, we want to figure out all the fail conditions (success conditions range from 0 to 15):

P (60%-effective drug fails "sixteen or more" rule) = \sum_{k = 0}^{15} (\binom{30}{k}) (0.60)^{k} (0.40)^{30 - k} = 0.1754

b. How often will the “sixteen or more” rule allow a 50%-effective drug to be perceived as a major breakthrough? 简单理解就是假突破

$p = 0.5$ ，we have 30 monkeys, we want to figure out all the success conditions(success conditions range from 16 to 30):

\begin{aligned} P (50%-effective PM-17 appears to be marketable) & = P (Sixteen or more successes occur) \\ = \sum_{k = 16}^{30} (\binom{30}{k}) (0.5)^{k} (0.5)^{30 - k} \\ = 0.43 \end{aligned}

example3

The junior mathematics class at Superior High School knows that the probability of making a 600 or greater on the SAT Reasoning Test in Mathematics is 0.231, while the similar probability for the Critical Reading Test is 0.191. 获得优秀数学分数的概率是0.231，获得优秀文学奖的概率是0.191.

Each group will select four students and have them take the respective test. The mathematics students will win the challenge if more of their members exceed 600 on the mathematics test than do the other students on the Critical Reading Test. 每个组选4个人，如果数学优秀的人数大于优秀文学的人数，则数学组赢，否则文学组赢

Assume M denote the number of mathematicians scores of 600 and more, CR denotes the similar number for the Critical Reading Test. It is indepent joint probability:

\begin{aligned} P (C R = 2, M = 3) & = \\ P (C R = 2) \cdot P (M = 3) & = [(\binom{4}{2}) (0.191)^{2} (0.809)^{2}] \cdot [(\binom{4}{3}) (0.231)^{3} (0.769)^{1}] \\ = (0.143) (0.038) = 0.0054 \end{aligned}

CR \ M	0	1	2	3	4
0	0.1498	0.1800	0.0811	0.0162	0.0012
1	0.1415	0.1700	0.0766	0.0153	0.0012
2	0.0501	0.0602	0.0271	0.0054	0.0004
3	0.0079	0.0095	0.0043	0.0009	0.0001
4	0.0005	0.0006	0.0003	0.0001	0.0000

Actually, The sum of the probabilities in the MATH win cells is 0.3775. The mathematics students need to study more probability.

Hypergeometric Distribution

Suppose an urn contains r red chips and w white chips, where $r + w = N$ . If $n$ chips are drawn out at random, without replacement, and if k denotes the number of red chips selected, then

P (k red chips are chosen) = \frac{(\binom{r}{k}) (\binom{w}{n - k})}{(\binom{N}{n})}

if replacement, 如果有放回 the question becomes Binomial distribution

where:

$(\binom{r}{k})$ : The number of ways to choose $k$ successes from r items.
$(\binom{w}{n - k})$ : The number of ways to choose $n - k$ failures from w items.
$(\binom{N}{n})$ : The total number of ways to choose n items from N .

example1

A tax collector, ﬁnding himself short of funds, delayed depositing a large property tax payment ten different times. The money was subsequently repaid, and the whole amount deposited in the proper account. The tip-off to this behavior was the delay of the deposit (bad behaviour!). During the period of these irregularities, there was a total of 470 tax collections. 一名税务征收员因资金短缺，将一笔大额财产税款的存款延迟了十次。此后该款项已偿还，并全额存入相应账户。这种行为的提示是存款延迟。在此期间，共进行了 470 次税收。

An auditing ﬁrm was preparing to do a routine annual audit of these transactions. They decided to randomly sample nineteen of the collections (approximately 4%) of the payments. The auditors would assume a pattern of malfeasance only if they saw three or more irregularities. What is the probability that three or more of the delayed deposits would be chosen in this sample? 一家审计公司准备对这些交易进行例行年度审计。他们决定随机抽查 19 笔收款. 审计人员只有在发现三个或三个以上的违规行为时，才会认为存在渎职行为。在这个样本中选择三笔或更多延迟存款的概率是多少？

Here, $N = 470, n = 19, r = 10, w = 460$ . In this case it is better to calculate the desired probability via the complement补集, that is,

1 - \frac{(\binom{10}{0}) (\binom{460}{19})}{(\binom{470}{19})} - \frac{(\binom{10}{1}) (\binom{460}{18})}{(\binom{470}{19})} - \frac{(\binom{10}{2}) (\binom{460}{17})}{(\binom{470}{19})}

example2

Biting into a plump, juicy apple is one of the innocent pleasures of autumn. Critical to that enjoyment is the ﬁrmness硬度 of the apple, a property that growers and shippers monitor closely. The apple industry goes so far as to set a lowest acceptable limit for ﬁrmness, which is measured (in lbs) by inserting a probe into the apple. For the Red Delicious variety, for example, ﬁrmness is supposed to be at least 12 lbs; in the state of Washington, wholesalers are not allowed to sell apples if more than 10% of their shipment falls below that 12-lb limit.

How can shippers demonstrate that their apples meet the 10% standard? Sampling as the only viable strategy.

Suppose, for example, a shipper has a supply of 144 apples. suppose there are actually 10 defective apples among the original 144, Since $\frac{10}{144} \times 100 = 6.9 %$ , that shipment would be suitable for sale because fewer than 10% failed to meet the ﬁrmness standard.

If we use Hypergeometric Distribution for sampling? We can calculate the possibility of Sample passes inspection:

\begin{aligned} P (Sample passes inspection) & = P (2 or fewer substandard apples are found) \\ = \frac{(\binom{10}{0}) (\binom{134}{15})}{(\binom{144}{15})} + \frac{(\binom{10}{1}) (\binom{134}{14})}{(\binom{144}{15})} + \frac{(\binom{10}{2}) (\binom{134}{13})}{(\binom{144}{15})} \\ = 0.320 + 0.401 + 0.208 = 0.929 \end{aligned}

Seems nice? But if the bad apples increase to 30, $21 %$ :

\begin{aligned} P (Sample passes inspection) & = \frac{(\binom{30}{0}) (\binom{114}{15})}{(\binom{144}{15})} + \frac{(\binom{30}{1}) (\binom{114}{14})}{(\binom{144}{15})} + \frac{(\binom{30}{2}) (\binom{114}{13})}{(\binom{144}{15})} \\ = 0.024 + 0.110 + 0.221 = 0.355 \end{aligned}

Seems worse than before, we have 36% of the time can pass the exam even though the bad standard.

Every sampling plan invariably allows for two kinds of errors : rejecting shipments that should be accepted and accepting shipments that should be rejected. The probabilities of committing these errors can be manipulated by redeﬁning the decision rule and/or changing the sample size. More detail refer to HYPOTHESIS TESTING.

Discrete Random Variables

Definition 3.3.1. Suppose that $S$ is a finite or countably infinite sample space. Let $p$ be a real-valued function defined for each element of $S$ such that

$0 \leq p (s)$ for each $s \in S$
$\sum_{s \in S} p (s) = 1$

Then $p$ is said to be a discrete probability function.

Definition 3.3.2. A function whose domain is a sample space $S$ and whose values form a finite or countably infinite set of real numbers is called a discrete random variable. We denote random variables by uppercase letters, often $X$ or $Y$ .

Definition 3.3.3. Associated with every discrete random variable $X$ is a probability density function (or pdf), denoted $p_{X} (k)$ , where

p_{X} (k) = P ({s \in S ∣ X (s) = k})

Note that $p_{X} (k) = 0$ for any $k$ not in the range of $X$ . For notational simplicity, we will usually delete all references to $s$ and $S$ and write $p_{X} (k) = P (X = k)$ .

example

Binomial distribution: $P (X = k) = p_{X} (k) = (\binom{n}{k}) p^{k} (1 - p)^{n - k}, k = 0, 1, \dots, n$
Hypergeometric Distribution: $P (X = k) = p_{X} (k) = \frac{(\binom{r}{k}) (\binom{w}{n - k})}{(\binom{r + w}{n})}$

Consider again the rolling of two dice. Let $i$ and $j$ denote the faces showing on the ﬁrst and second die, respectively, and deﬁne the random variable X to be the sum of the two faces: $X (i, j) = i + j$ . Find $p_{X} (k)$ .

Assume $k = 5$ , when $X (s) = 5$ , $s = {(1, 4), (4, 1), (2, 3), (3, 2)} \in S$

\begin{aligned} P (X = 5) & = p_{X} (5) = P ({s \in S ∣ X (s) = 5}) \\ = P [(1, 4), (4, 1), (2, 3), (3, 2)] \\ = P (1, 4) + P (4, 1) + P (2, 3) + P (3, 2) \\ = \frac{1}{36} + \frac{1}{36} + \frac{1}{36} + \frac{1}{36} \\ = \frac{4}{36} \end{aligned}

$k$	$p_{X} (k)$	$k$	$p_{X} (k)$
2	$1 / 36$	8	$5 / 36$
3	$2 / 36$	9	$4 / 36$
4	$3 / 36$	10	$3 / 36$
5	$4 / 36$	11	$2 / 36$
6	$5 / 36$	12	$1 / 36$
7	$6 / 36$

Discrete Cumulative Distribution Function

Definition 3.3.4. Let $X$ be a discrete random variable. For any real number $t$ , the probability that $X$ takes on a value $\leq t$ is the cumulative distribution function (cdf) of $X$ [written $F_{X} (t)$ ]. In formal notation, $F_{X} (t) = P ({s \in S ∣ X (s) \leq t})$ . As was the case with pdfs, references to $s$ and $S$ are typically deleted, and the cdf is written $F_{X} (t) = P (X \leq t)$ .

example

Suppose that two fair dice are rolled. Let the random variable $X$ denote the larger of the two faces showing:

(a) Find $F_{X} (t)$ for $t = 1, 2, \dots, 6$

\begin{aligned} F_{X} (t) & = P (X \leq t) \\ = P (Max (i, j) \leq t) \\ = P (i \leq t and j \leq t) \\ = P (i \leq t) \cdot P (j \leq t) \\ = \frac{t}{6} \cdot \frac{t}{6} \\ = \frac{t^{2}}{36}, t = 1, 2, 3, 4, 5, 6 \end{aligned}

(b) Find $F_{X} (2.5)$ .

\begin{aligned} P (X \leq 2.5) & = P (X \leq 2) + P (2 < X \leq 2.5) \\ = F_{X} (2) + 0 \\ s o, F_{X} (2.5) & = F_{X} (2) = \frac{2^{2}}{36} = \frac{1}{9} \end{aligned}

Continuous Random Variables

Definition 3.4.1. A probability function $P$ on a set of real numbers $S$ is called continuous if there exists a function $f (t)$ such that for any closed interval $[a, b] \subset S$ ,

P ([a, b]) = \int_{a}^{b} f (t) d t .

Comment If a probability function $P$ satisfies Definition 3.4.1, then

P (A) = \int_{A} f (t) d t

for any set $A$ where the integral is defined.

Conversely, suppose a function $f (t)$ has the two properties:

$f (t) \geq 0$ for all $t$ .
$\int_{- \infty}^{\infty} f (t) d t = 1$ .

Fitting $f (t)$ to Data: The Density-Scaled Histogram

We can use a continuous probability function to approximate an integervalued discrete probability model

example

Suppose an electronic surveillance monitor监视器 is turned on brieﬂy at the beginning of every hour and has a 0.905 probability of working properly, regardless of how long it has remained in service.

p_{X} (k) = P (X = k) = (0.905)^{k - 1} (1 - 0.905)

We can draw the hisgram of $p_{X} (k)$ . Using curve $ y = 0.1e^{−0.1x}$ is superimposed on 叠加 the graph of $p_{X} (k)$ , this curve is our sought-after追求的 alternative to $p (s)$ for continuous sample spaces.

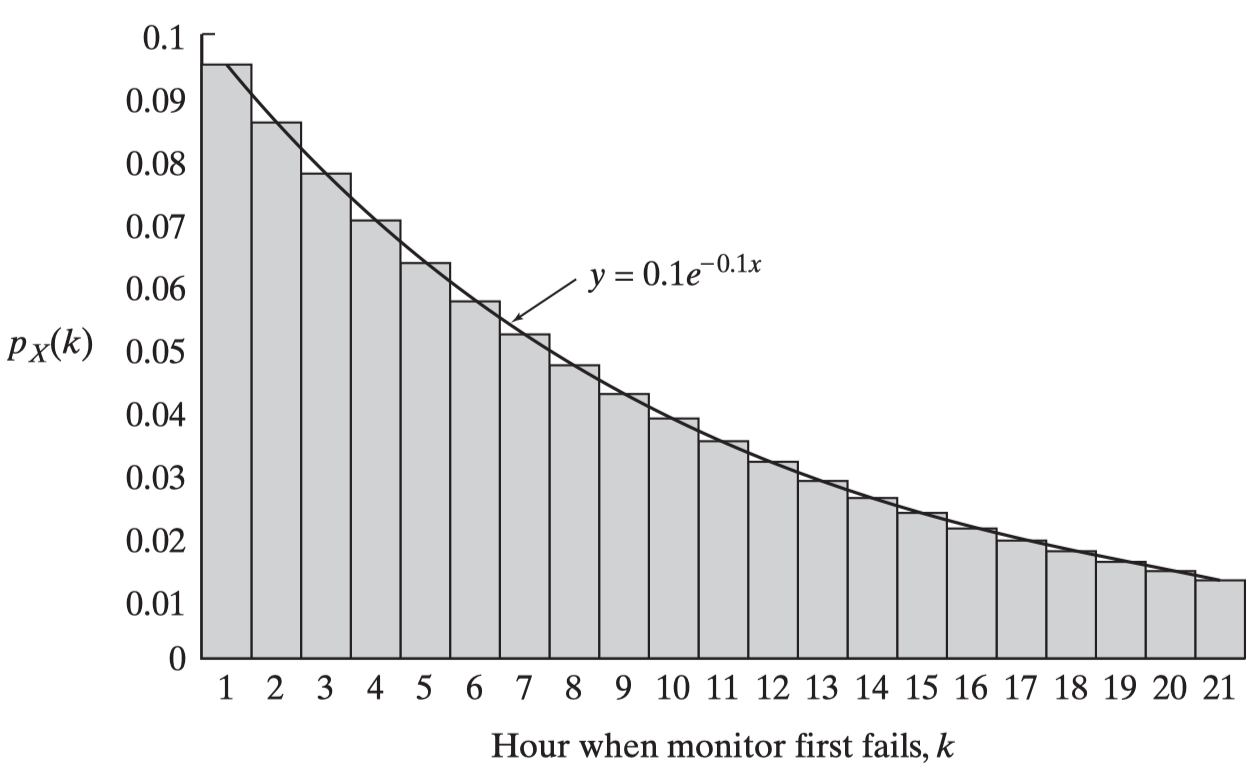
image-2024110383308072 PM

example2

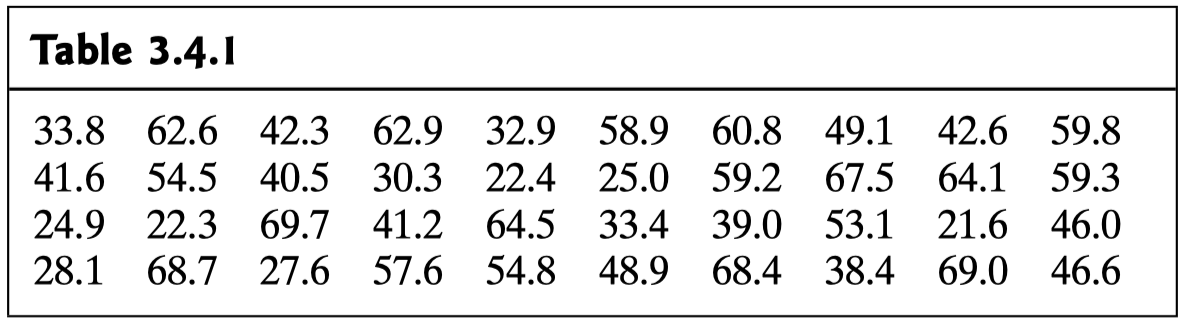
image-2024110390735931 PM

suppose we have reason to believe that these forty y i ’s may be a random sample from a uniform probability function 均匀概率函数 deﬁned over the interval [20, 70]

f (t) = \frac{1}{70 - 20} = \frac{1}{50}, 20 \leq t \leq 70

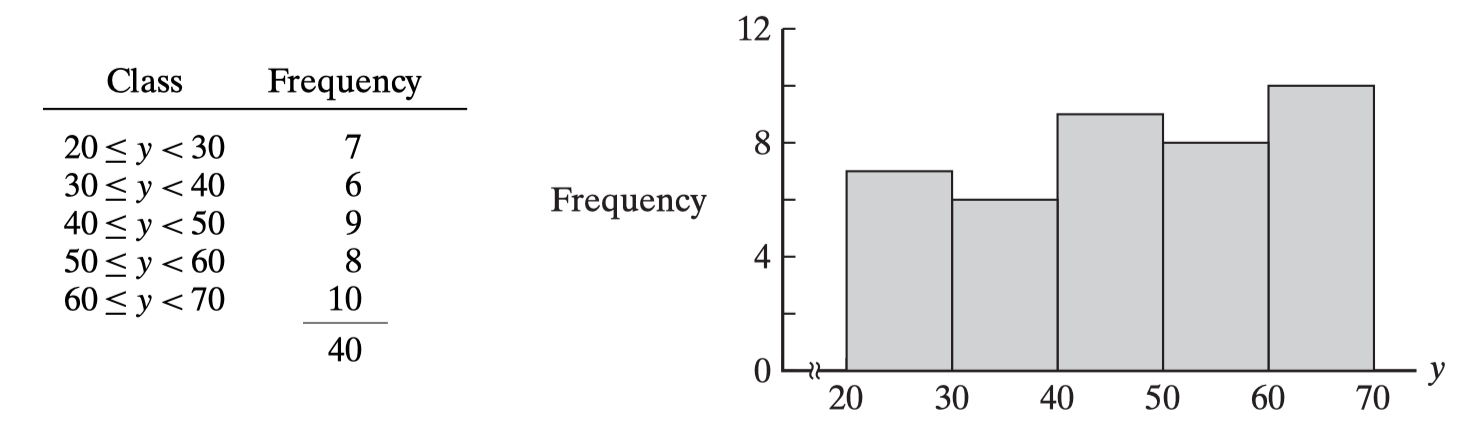
image-2024110391158587 PM

In Frequency histogram, the sum of the areas is not 1, we can use formula to calculate Density:

density (of a class) = \frac{class frequency}{total no. of observations \times class width}

For example, integrating积分 that constant over the interval [20,30) would give $\frac{7}{40}$ , which is possibility of this interval, so the density should be given by dividing the probability by the length 10, thus the density is $\frac{7}{40 \times 10}$

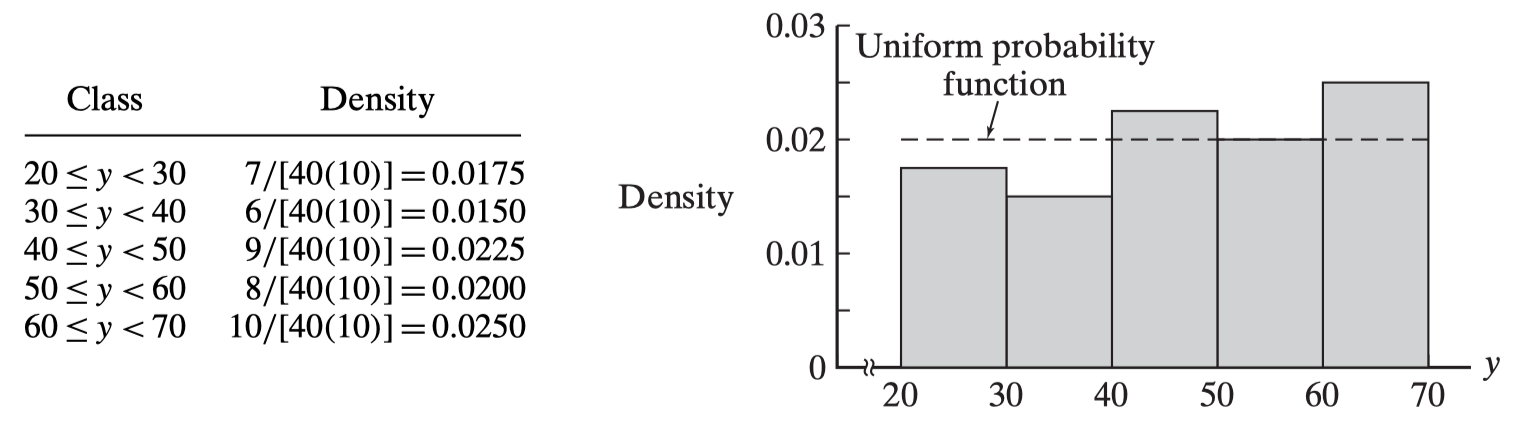
image-2024110392108194 PM

Continuous Probability Density Functions (pdf)

Definition 3.4.2. Let $Y$ be a function from a sample space $S$ to the real numbers. The function $Y$ is called a continuous random variable if there exists a function $f_{Y} (y)$ such that for any real numbers $a$ and $b$ with $a < b$

P (a \leq Y \leq b) = \int_{a}^{b} f_{Y} (y) d y

The function $f_{Y} (y)$ is the probability density function (pdf) for $Y$ .
As in the discrete case, the cumulative distribution function (cdf) is defined by

F_{Y} (y) = P (Y \leq y) = \int_{- \infin}^{b} f_{Y} (y) d y

Expected Values

Definition 3.5.1. Let $X$ be a discrete random variable with probability function $p_{X} (k)$ . The expected value of $X$ is denoted $E (X)$ (or sometimes $μ$ or $μ_{X}$ ) and is given by

E (X) = μ = μ_{X} = \sum_{all k} k \cdot p_{X} (k)

Similarly, if $Y$ is a continuous random variable with pdf $f_{Y} (y)$ ,

E (Y) = μ = μ_{Y} = \int_{- \infty}^{\infty} y \cdot f_{Y} (y) d y

Comment We assume that both the sum and the integral in Definition 3.5.1 converge absolutely:

\sum_{all k} | k | p_{X} (k) < \infty and \int_{- \infty}^{\infty} | y | f_{Y} (y) d y < \infty

If not, we say that the random variable has no finite expected value. One immediate reason for requiring absolute convergence is that a convergent sum that is not absolutely convergent depends on the order in which the terms are added, and order should obviously not be a consideration when defining an average.

Riemann Series Theorem (Rearrangement Theorem) 黎曼数列定理（重排定理）
黎曼数列定理指出，对于任何有条件收敛的数列，都可以重新排列项，使其和为任何实数，甚至发散。这一性质表明，如果没有绝对收敛，和（或积分）就缺少一个稳定、唯一的值。它可以根据项相加的顺序产生不同的结果。对于定义一个有意义的随机变量的期望值来说，这种对顺序的依赖是有问题的，因为结果应该是唯一的，并且在项的重新排列下是不变的。

Binomial random variable $X$ with parameters $n$ and $p$ . Then $E (X) = n p$ .
Hypergeometric random variable $X$ with parameters $r$ , $w$ , and $n$ . That is, suppose an urn contains $r$ red balls and $w$ white balls. A sample of size $n$ is drawn simultaneously from the urn. Let $X$ be the number of red balls in the sample. Then $E (X) = \frac{r n}{r + w}$

example

Among the more common versions of the “numbers” racket is a game called D.J., its name deriving from the fact that the winning ticket is determined from Dow Jones averages.

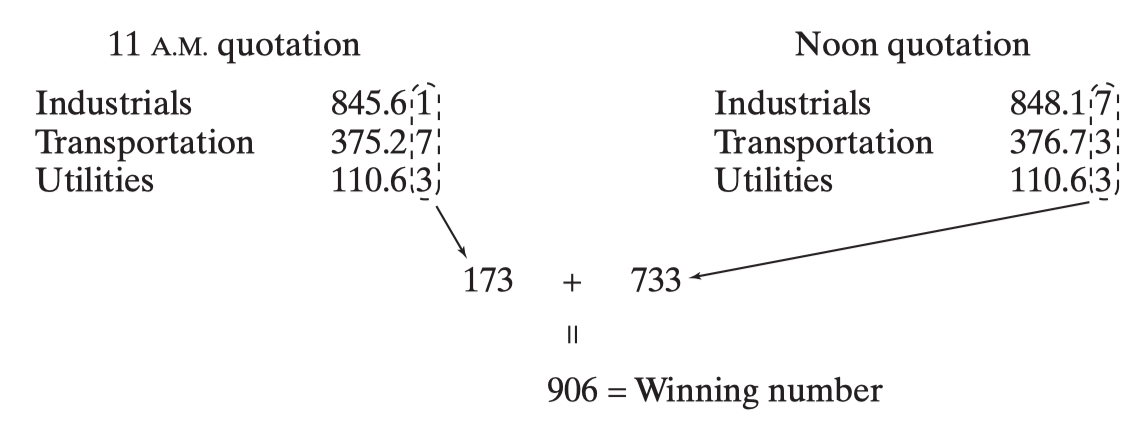
image-20241103101650618 PM

Let $p$ denote the probability of our number being the winner and let $X$ denote our earnings. The:

X = {\begin{cases} 3500 & with probability p \\ - 5 & with probability 1 - p \end{cases} E (X) = 3500 \cdot p - 5 \cdot (1 - p)

E (X) = 3500 \cdot (\frac{1}{1000}) - 5 \cdot (\frac{999}{1000}) = - 1.50

On the average, then, we lose $1.50 on a $5.00 bet.

example2

Consider the following game. A fair coin is flipped until the first tail appears; we win $2 if it appears on the first toss, $4 if it appears on the second toss, and, in general, $$ 2^{k}$ if it first occurs on the $k$ th toss. Let the random variable $X$ denote our winnings. How much should we have to pay in order for this to be a fair game? [Note: A fair game is one where the difference between the ante and $E (X)$ is 0.]

Known as the St. Petersburg paradox, this problem has a rather unusual answer.

First, note that

p_{X} (2^{k}) = P (X = 2^{k}) = \frac{1}{2^{k}}, k = 1, 2, \dots

Therefore,

E (X) = \sum_{all k} 2^{k} p_{X} (2^{k}) = \sum_{k = 1}^{\infty} 2^{k} \cdot \frac{1}{2^{k}} = 1 + 1 + 1 + \dots

That is, $X$ does not have a ﬁnite expected value, so in order for this game to be fair, our ante赌注 would have to be an inﬁnite amount of money!

STATISTICS ​

Random variables ​

Binomial distribution ​

example1 ​

example2 ​

example3 ​

Hypergeometric Distribution ​

example1 ​

example2 ​

Discrete Random Variables ​

example ​

Discrete Cumulative Distribution Function ​

example ​

Continuous Random Variables ​

Fitting f(t) to Data: The Density-Scaled Histogram ​

example ​

example2 ​

Continuous Probability Density Functions (pdf) ​

Expected Values ​

example ​

example2 ​

STATISTICS

Random variables

Binomial distribution

example1

example2

example3

Hypergeometric Distribution

example1

example2

Discrete Random Variables

example

Discrete Cumulative Distribution Function

example

Continuous Random Variables

Fitting $f (t)$ to Data: The Density-Scaled Histogram

example

example2

Continuous Probability Density Functions (pdf)

Expected Values

example

example2